84 Largest Rectangle in Histogram (David)

This post is an in-depth explanation of the Largest Rectangle in Histogram problem from LeetCode based on this solution by user dietpepsi:

Given n non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

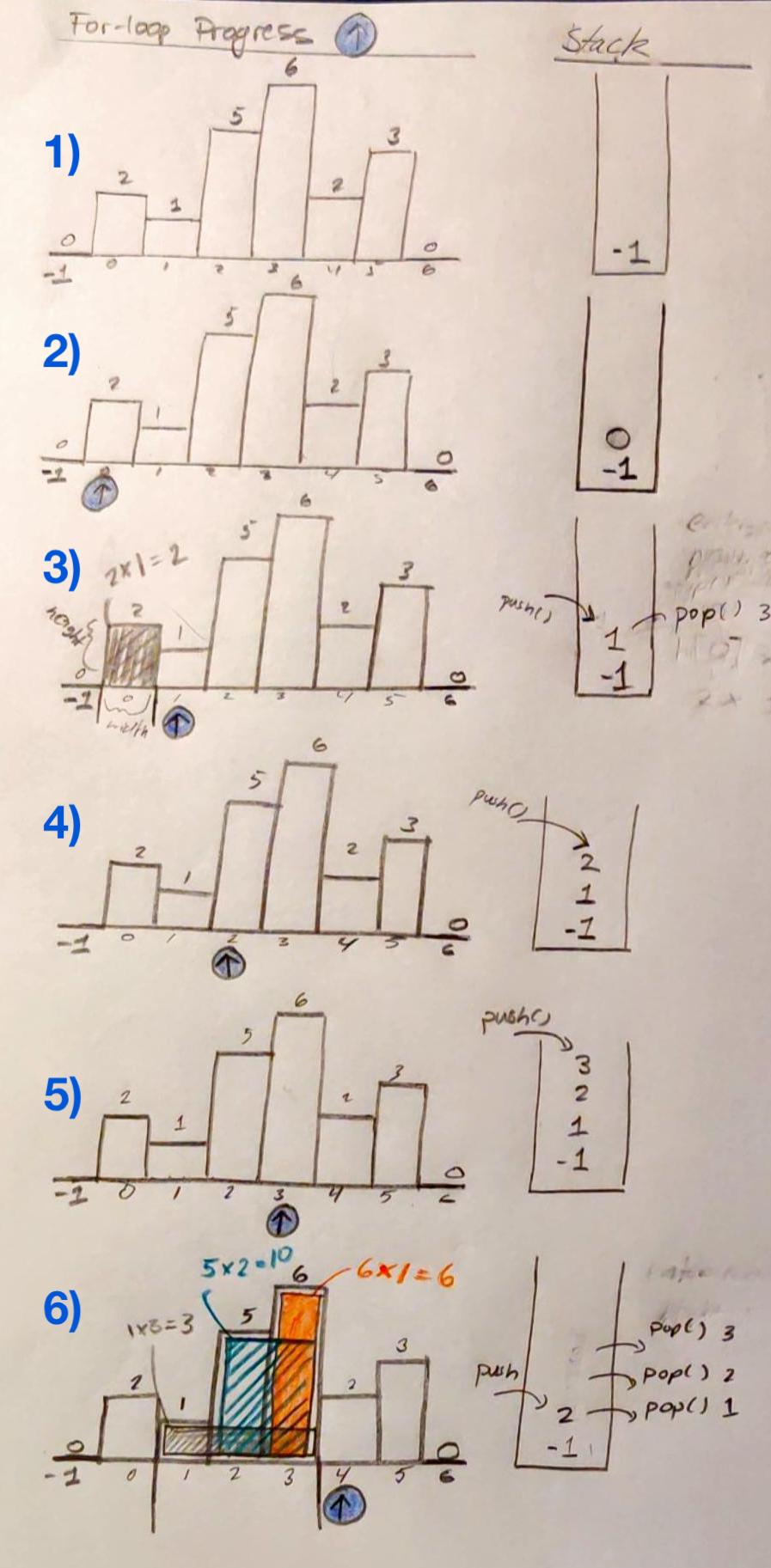
Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

The largest rectangle is shown in the shaded area, which has area = 10 unit.

Example:

Input: [2,1,5,6,2,3] Output: 10

This problem can be solved with a stack approach with O(n) time complexity. Parentheses-matching problems are commonly solved with stack-based approaches, and they are intuitive to understand. So, it can be useful to think of the Largest Rectangle in Histogram problem as an instance of a parentheses-matching problem, only instead of parentheses, you will match certain histogram bars. All rectangular areas in the histogram have one thing in common; they are book-ended by two bars (one on the right side, and one on the left side) which are smaller than the middle bars. In the example above, histogram bars with height 5 and 6 are caught between bars with height 1 and 2, thus forming a 5x2=10 rectangular area.

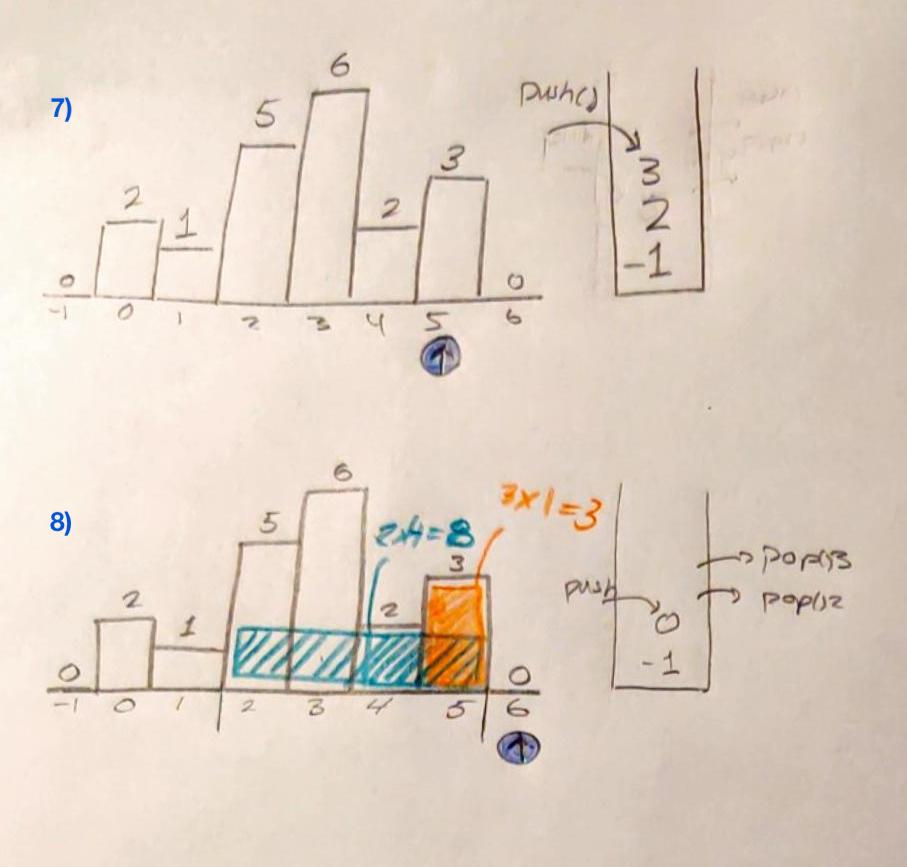
Traverse the histogram and add bar indices to the stack. In the code below, we traverse the histogram from left to right (→) in a for loop, adding a histogram’s bar index to the stack whenever the height of the current bar in the for loop is greater than or equal to the bar already on the stack. So, bars placed on the stack will be increasing or staying the same in terms of height; this property is necessary to because the rectangle areas with the height of the smaller bars on the left can extend into the taller bars on the right (see gray rectangle in step 6 shown below for a reference image.)

Stop traversing when you find a bar smaller than your previous bar. The parsing, i.e. the for loop, must stop as soon as the height of the bars decreases. A decreasing histogram bar constitutes our “right parentheses” and the previous smallest bar consitutes our left parentheses. At that point, where we encounter our “right parentheses” we enter a while loop to find the rectangular areas under the histogram bars we’ve been accumulating in the stack. The bars on the stack will only be those that are between our left and right parentheses bars.

Calculate the area under that portion of the histogram after you stop the for loop. We pop data off the stack and calculate the maximum area in the body of the while loop below. In the body of the while loop, i remains fixed, while stack[-1] represents an index farther and farther to the left as items are popped off the stack. The effect is that the smaller-height bars encountered earlier in the parsing have a greater width than the taller bars encountered later (again, see step 6 in the image below for reference.) In treating the histogram as a parentheses-matching problem, it becomes necessary to establish outer-most “parentheses” represented by the dummy bars with height zero at indices -1 and 6. These dummy bars allow us to find the width of the histogram area under consideration when we consider the leftmost or rightmost histogram bars on the plot. These parentheses exist The variable ans stores the height of largest area encountered so far. So, ans = max(ans, h * w) finds whether the previous maximum rectangular area, ans, or the current rectangular area under consideration, h * w, is greater and assigns ans to that greater value.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

def largestRectangleArea(self, height):
    height.append(0)
    stack = [-1]
    ans = 0
    # traverse the histogram and add bar indices to the stack
    for i in range(len(height)):

        # whenever you encounter a bar smaller than the previous bar, 
        # stop traversing (and perform the while loop) 
        while height[i] < height[stack[-1]]:

            # calculate the area under that portion of the histogram 
            h = height[stack.pop()]
            w = i - stack[-1] - 1
            ans = max(ans, h * w)

        stack.append(i)
    height.pop()
    return ans

Like this post? Share on: Twitter ❄ Facebook ❄ Email